ECUACIONES POLINÓMICAS
Ecuaciones de primer grado con una incógnita
Una ecuación de primer grado con una incógnita es una igualdad entre polinomios con una sola variable de primer grado.
Para resolver una ecuación de primer grado con una incógnita:
El número máximo de soluciones de una ecuación de primer grado con una incógnita es uno (como indica su grado). Antes del último paso (despejar la incógnita) sabremos si la ecuación va a tener o no solución, ya que:
Si la ecuación no tiene el aspecto del ejemplo por tener paréntesis y/o denominadores, antes hay que quitarlos para poder resolverla:
CRUCIGRAMA CON ECUACIONES DE PRIMER GRADO (NIVEL 3): Con esta actividad de Hot Potatoes podrás practicar la resolución de ecuaciones de primer grado con paréntesis y denominadores
Ecuaciones de segundo grado con una incógnita
Una ecuación de segundo grado con una incógnita es una igualdad entre polinomios con una sola variable en la que al menos uno de ellos es de segundo grado. La forma canónica de una ecuación completa de segundo grado es el siguiente:
Puede faltar alguno de los términos, dando lugar a una ecuación incompleta de segundo grado. Hay tres casos:
Para resolver una ecuación de segundo grado con una incógnita, según sea completa o incompleta:
El número máximo de soluciones de una ecuación de segundo grado con una incógnita es dos (como indica su grado). El discriminante es el que determina el número de soluciones:
Si la ecuación no estuviera escrita en forma canónica, primero se opera la ecuación aplicando lo mismo que lo indicado para primer grado hasta obtener el aspecto general y después se resuelve según el caso.
Ecuaciones polinómicas de grado mayor o igual que tres
Una ecuación polinómica de grado mayor o igual que tres es una igualdad entre polinomios con una sola variable en la que al menos uno de ellos es de tercer grado o superior. El aspecto general de una ecuación polinómica de grado mayor o igual que tres es el siguiente:
Una ecuación polinómica de grado mayor o igual que tres es una igualdad entre polinomios con una sola variable en la que al menos uno de ellos es de tercer grado o superior. El aspecto general de una ecuación polinómica de grado mayor o igual que tres es el siguiente:
Para resolver una ecuación polinómica de grado mayor o igual que tres no tenemos más que factorizar el polinomio, ya que las soluciones de este tipo de ecuaciones son las raíces del polinomio correspondiente.
El número máximo de soluciones de una ecuación polinómica de grado mayor o igual que tres es el que indica su grado.
Si la ecuación no tuviera el aspecto general antes indicado, primero se opera la ecuación aplicando lo mismo que lo indicado para primer grado hasta obtener el aspecto general y después se factoriza.
Ecuaciones bicuadradas
Una ecuación bicuadrada es una igualdad entre polinomios con una sola variable de cuarto grado sólo con términos pares. El aspecto general de una ecuación bicuadrada es el siguiente:
Al tener sólo términos pares, existe otro procedimiento para resolverlas más rápido que el anterior, que consiste en hacer un cambio de variable para convertirla en una de segundo grado:










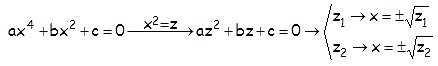
Comentarios
Publicar un comentario